Défi d’horlogerie...
Pour ne pas trop vous distraire si vous révisez vos examens, voici un petit défi qui vous permettra de garder le cerveau connecté.
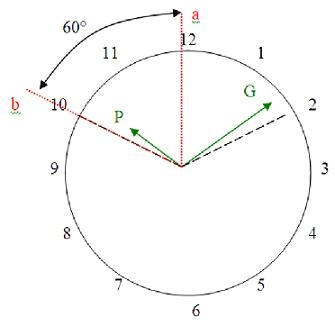
Exposé du problème : Vous avez tous déjà vu dans les vitrines des bijoutiers les montres réglées à peu près à 10 h 10, parce que c’est à cette heure là que leur position est la plus esthétique. Le défi consiste à définir de façon mathématique à quelle heure précise la petite et la grande aiguille forment le même angle par rapport à l’axe vertical. On prendra l’hypothèse que leur déplacement est constant. Bonne réflexion ! __________________________________________________________________________________ Notre solution : On raisonne en degrés, que l’on convertira en heures à la fin. On nomme x la valeur du déplacement de la grande aiguille (G) en degrés. Si l’on considère qu’elle débute sa course à 10h pile, x désigne donc son éloignement par rapport à l’axe a (c’est la valeur de l’angle entre a et G). On exprime ensuite le déplacement de la petite aiguille (P) en fonction de ce même x. On trouve x/12, c'est-à-dire que quand G parcourt x degrés, P en parcourt x/12 (vérifiez avec des valeurs). Mais attention, car la valeur x/12 désigne l’angle entre b et P, et non l’angle entre P et a que l’on cherche. Pour obtenir cet angle, il faut faire 60 – x/12 (60° étant la valeur de l’angle entre b et a). P et G seront donc parfaitement symétriques lorsque l’angle entre P et a sera le même que celui entre a et G ; c'est-à-dire quand x vaudra 60 – x/12. On résout l’équation x = 60 – x/12 et obtient x = 55,384615° Donc quand G a parcouru 55,384615° depuis l’axe a ; P a parcouru un angle tel, qu’il ne lui reste plus qu’à parcourir 55,384615° jusqu’à a. Il n’y a plus qu’à convertir cet angle en heures. On sait que P indique toujours en gros 10h. Intéressons nous à G. Sur le cadran, une amplitude de 5 minutes correspond à un angle de 30°. Par un produit en croix, on peut donc dire que x en minutes vaut : (55,384615 x 5)/30 = 9,23 min. Ce n’est pas tout à fait fini, car le « 0,23 » est une valeur décimale (comme s’il y avait 100 secondes dans une minute). Il faut convertir cette valeur en secondes « normales » : (23x60)/100 = 13,80. La réponse est donc : 10 h 9min 13 sec 80’’.